Abstract:

DDSAnalytics is an analytics company that specializes in talent management solutions for Fortune 100 companies. Talent management is the iterative process of developing and retaining employees. To gain a competitive edge over its competition, DDSAnalytics is planning to leverage data science for talent management. The executive leadership has identified predicting employee turnover as its first application of data science for talent management. Before the business green lights the project, they have tasked my data science team to conduct an analysis of existing employee data.

Watch me (quickly) present these findings on YouTube!

Objectives:

Target Audience:

Data Analysis & Findings:

Import & Validate data:

A simple sum of missing values returns 0, which means this dataset is clean and we can start our EDA!

Exploratory Data Analysis

In Exploratory Data Analysis (EDA), we’re looking for correlation among 36 original features. We are primarily looking for features that we can use to predict attrition in the workplace.

data <- read.csv("./data/CaseStudy2-data.csv", header=T)
#data <- read.csv("./data/CaseStudy2CompSet No Attrition.csv", header=T)
oData <- data # Save original dataset

# Check for missing values:
MissingValues <- sapply(data, function(x) sum(is.na(x)))
sum(MissingValues)
## [1] 0
# One-hot encode categorical variables:
data$Attrition <- ifelse(data$Attrition == "Yes",1,0)
data$OverTime <- ifelse(data$OverTime == "Yes",1,0)
data$Gender <- ifelse(data$Gender == "Male",1,0)
data$BusinessTravel <- as.numeric(factor(data$BusinessTravel, 
                                         levels=c("Non-Travel", "Travel_Rarely", "Travel_Frequently"))) -1
data$HumanResources <- ifelse(data$Department == "Human Resources",1,0)
data$ResearchDevelopment <- ifelse(data$Department == "Research & Development",1,0)
data$Sales <- ifelse(data$Department == "Sales",1,0)
data$Single <- ifelse(data$MaritalStatus == "Single",1,0)
data$Married <- ifelse(data$MaritalStatus == "Married",1,0)
data$Divorced <- ifelse(data$MaritalStatus == "Divorced",1,0)
data$EdHumanResources <- ifelse(data$EducationField == "Human Resources",1,0)
data$EdLifeSciences <- ifelse(data$EducationField == "Life Sciences",1,0)
data$EdMedical <- ifelse(data$EducationField == "Medical",1,0)
data$EdMarketing <- ifelse(data$EducationField == "Marketing",1,0)
data$EdTechnicalDegree <- ifelse(data$EducationField == "Technical Degree",1,0)
data$EdOther <- ifelse(data$EducationField == "Other",1,0)
data$JobSalesExecutive <- ifelse(data$JobRole == "Sales Executive",1,0)
data$JobResearchDirector <- ifelse(data$JobRole == "Research Director",1,0)
data$JobManufacturingDirector <- ifelse(data$JobRole == "Manufacturing Director",1,0)
data$JobResearchScientist <- ifelse(data$JobRole == "Research Scientist",1,0)
data$JobSalesExecutive <- ifelse(data$JobRole == "Sales Executive",1,0)
data$JobSalesRepresentative <- ifelse(data$JobRole == "Sales Representative",1,0)
data$JobManager <- ifelse(data$JobRole == "Manager",1,0)
data$JobHealthcareRepresentative <- ifelse(data$JobRole == "Healthcare Representative",1,0)
data$JobHumanResources <- ifelse(data$JobRole == "Human Resources",1,0)
data$JobLaboratoryTechnician <- ifelse(data$JobRole == "Laboratory Technician",1,0)

Continuous Data:

# Visualize continuous data:
pIncome <- data %>% ggplot(aes(MonthlyIncome, Attrition)) + geom_smooth() 
pDistance <- data %>% ggplot(aes(DistanceFromHome, Attrition)) + geom_smooth()
pSalaryHike <- data %>% ggplot(aes(PercentSalaryHike, Attrition)) + geom_smooth()
pCompanies <- data %>% ggplot(aes(NumCompaniesWorked, Attrition)) + geom_smooth()
pDaily <- data %>% ggplot(aes(DailyRate, Attrition)) + geom_smooth() 
pHourly <- data %>% ggplot(aes(HourlyRate, Attrition)) + geom_smooth()
pMonthly <- data %>% ggplot(aes(MonthlyRate, Attrition)) + geom_smooth()
pAge <- data %>% ggplot(aes(Age, Attrition)) + geom_smooth()
pYearsCompany <- data %>% ggplot(aes(YearsAtCompany, Attrition)) + geom_smooth()
pYearsRole <- data %>% ggplot(aes(YearsInCurrentRole, Attrition)) + geom_smooth()
pPromotion <- data %>% ggplot(aes(YearsSinceLastPromotion, Attrition)) + geom_smooth()
pYearsManager <- data %>% ggplot(aes(YearsWithCurrManager, Attrition)) + geom_smooth()
pYearsWorking <- data %>% ggplot(aes(TotalWorkingYears, Attrition)) + geom_smooth()
grid.arrange(pIncome,pDistance,pSalaryHike,pCompanies,pDaily,pHourly,pMonthly,pAge,pYearsCompany,pYearsRole,pPromotion,pYearsManager,pYearsWorking, ncol=4, nrow=4)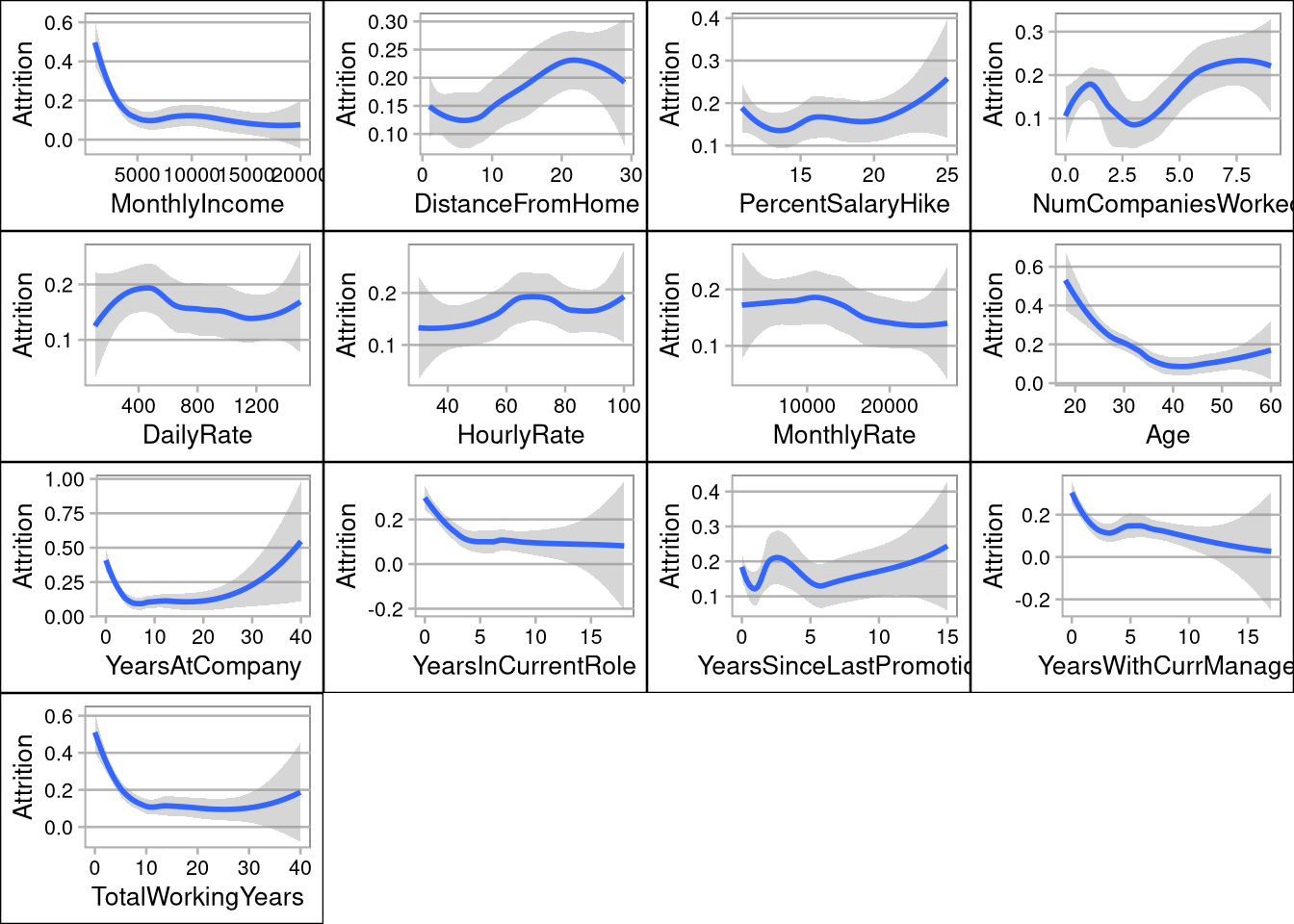

Ordinal Data:

# Visualize ordinal data:
pJobSat <- data %>% ggplot(aes(JobSatisfaction, Attrition)) + geom_smooth()
pJobLevel <- data %>% ggplot(aes(JobLevel, Attrition)) + geom_smooth()
pJobInvolvement <- data %>% ggplot(aes(JobInvolvement, Attrition)) + geom_smooth()
pTraining <- data %>% ggplot(aes(TrainingTimesLastYear, Attrition)) + geom_smooth()
pStock <- data %>% ggplot(aes(StockOptionLevel, Attrition)) + geom_smooth()
pTravel <- data %>% ggplot(aes(BusinessTravel, Attrition)) + geom_smooth()
pEducation <- data %>% ggplot(aes(Education, Attrition)) + geom_smooth()
pRelationship <- data %>% ggplot(aes(RelationshipSatisfaction, Attrition)) + geom_smooth()
pWorkLife <- data %>% ggplot(aes(WorkLifeBalance, Attrition)) + geom_smooth()
grid.arrange(pJobSat,pJobLevel,pJobInvolvement,pTraining,pStock,pTravel,pEducation,pRelationship,pWorkLife, ncol=3, nrow=3)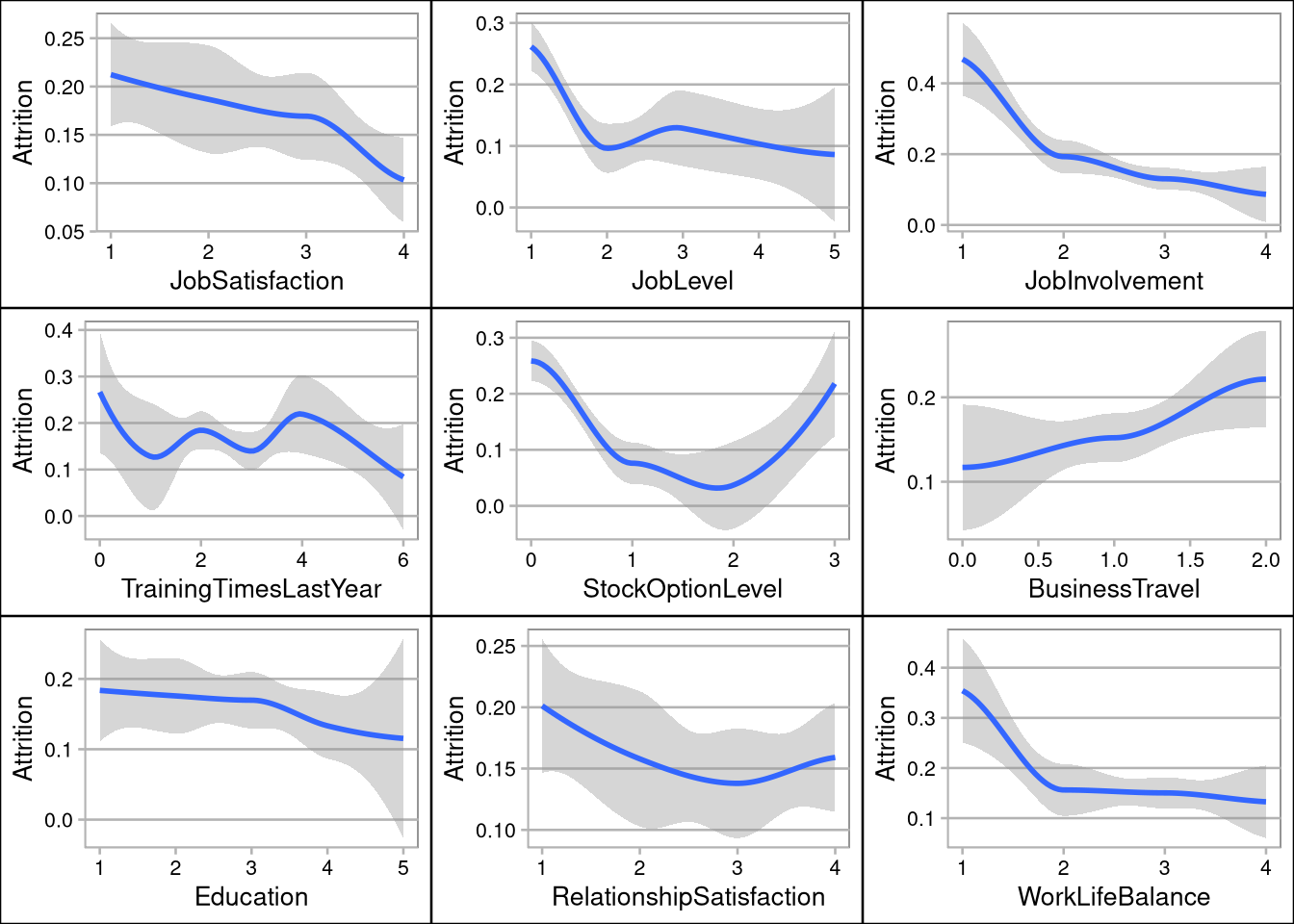

Categorical Data:

# Visualize categorical data:
pAttrition <- oData %>% group_by(Attrition) %>% summarise(count = n()) %>% 
    mutate(Percent = (count / sum(count))*100) %>% 
    ggplot() + geom_bar(aes(y=Percent, x=Attrition, fill=Attrition), stat = "identity")
pDept <- oData %>% ggplot(aes(Department, fill=Attrition)) + geom_bar()  + coord_flip()
pMarital <- oData %>% ggplot(aes(MaritalStatus, fill=Attrition)) + geom_bar()
pGender <- oData %>% ggplot(aes(Gender, fill=Attrition)) + geom_bar()
grid.arrange(pAttrition, pDept, pMarital,pGender, ncol=2, nrow=2)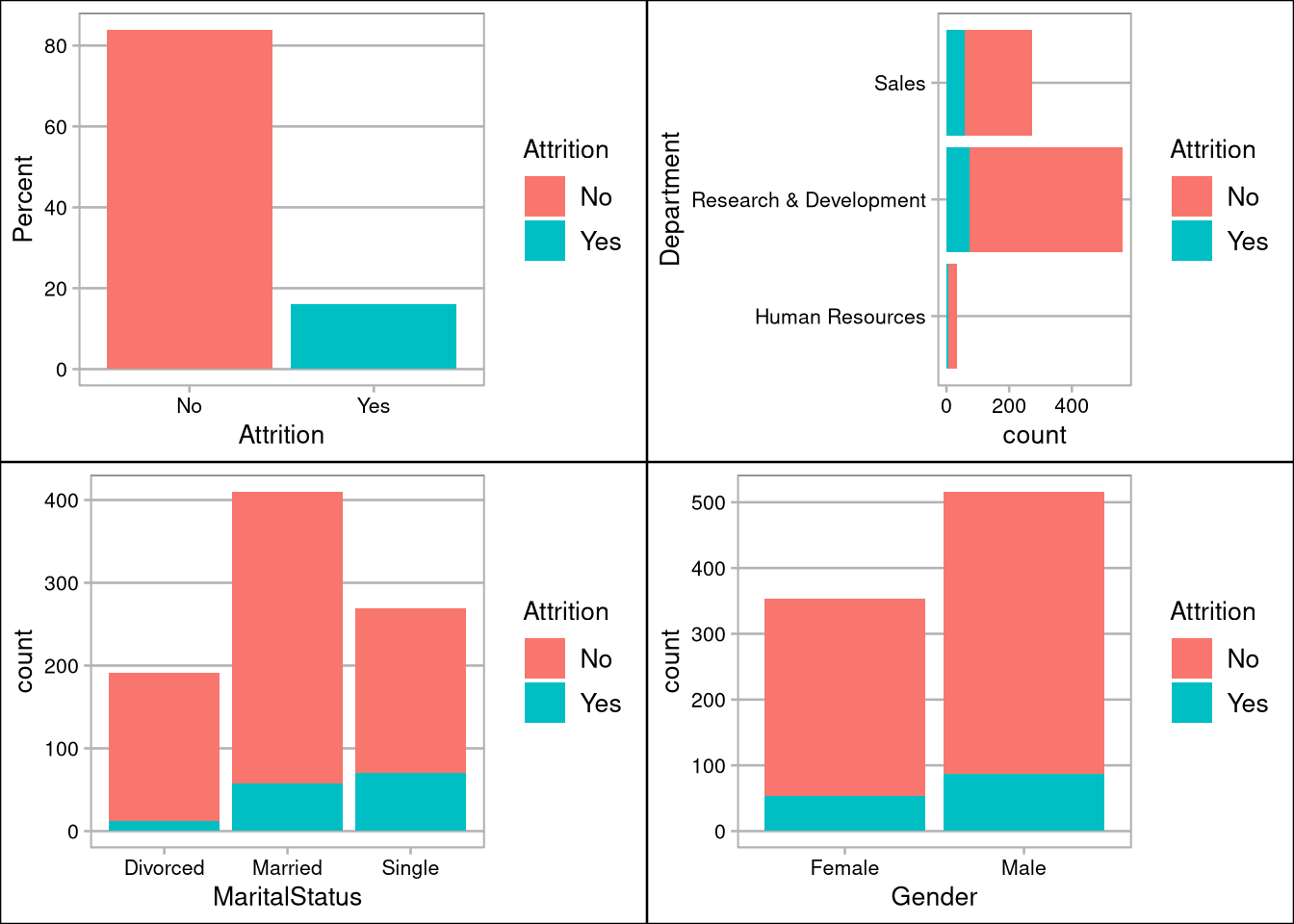

oData %>% ggplot(aes(JobRole, fill=Attrition)) + geom_bar() + coord_flip() + coord_flip() +  labs(title="Attrition by Job Role", y="Employees")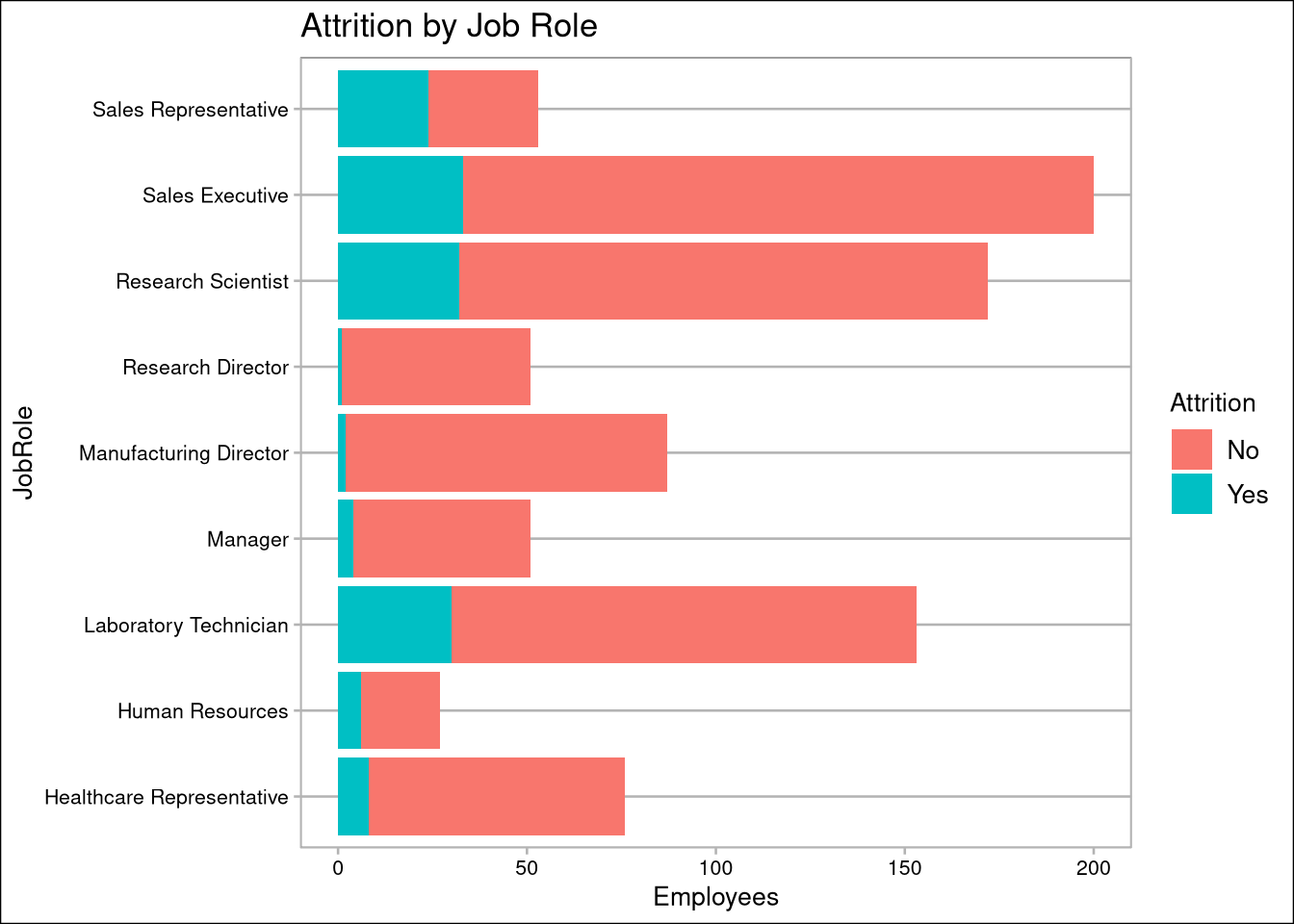

oData %>% ggplot(aes(EducationField)) + geom_bar(aes(fill=Attrition))  + coord_flip() + labs(title="Attrition by Educational Field", y="Employees")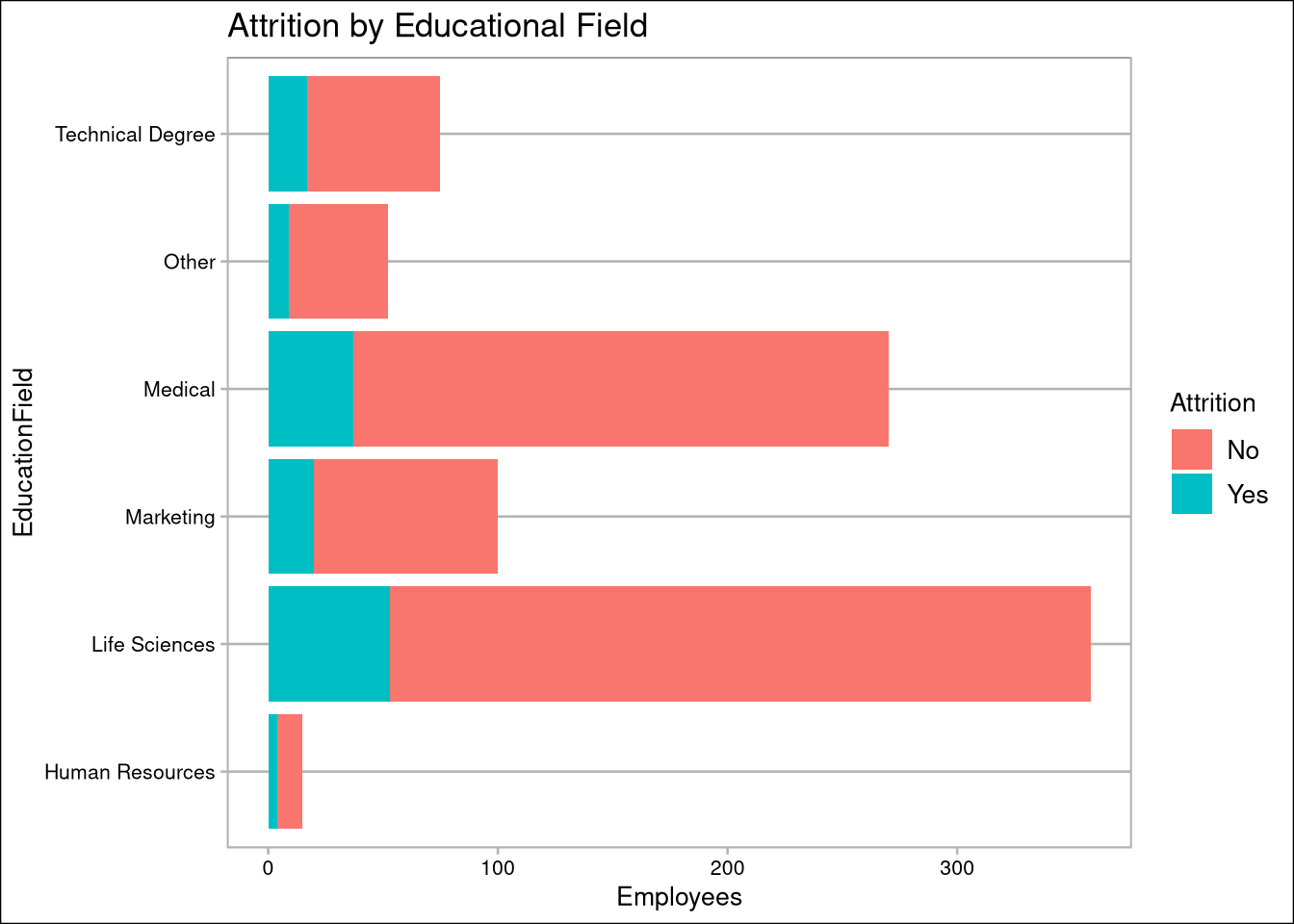

Feature Engineering

Feature engineering is designed to improve correlation by combining like type features, or slicing the data into distinct populations. I am going to use it to binary encode the categorical data to allow me to use Logistical Regression and improve performance in the KNN algorithm while predicting employee attrition and salary.

# binary encode ordinal variables 
data$LessThan5k <- ifelse(data$MonthlyIncome < 5000, 1, 0)
data$NewWorker <- ifelse(data$NumCompaniesWorked <=1, 1, 0)
data$LowLevel <- ifelse(data$JobLevel == 1, 1, 0)
data$NewHire <- ifelse(data$YearsAtCompany <4, 1, 0)
data$WorkedOver30 <- ifelse(data$TotalWorkingYears >=30, 1, 0)
data$Uninvolved <- ifelse(data$JobInvolvement <2, 1, 0)
data$NewToRole <- ifelse(data$YearsInCurrentRole <=1, 1, 0)
data$Unbalanced <- ifelse(data$WorkLifeBalance <2, 1, 0)
data$SalaryHike <- ifelse(data$PercentSalaryHike  >20, 1, 0)
data$HighlySatisfied <- ifelse(data$JobSatisfaction == 4, 1, 0)
data$LongCommute <- ifelse(data$DistanceFromHome >= 15, 1, 0)
data$AgeUnder40 <- ifelse(data$Age <40, 1, 0)
data$DueForPromotion <- ifelse(!data$YearsSinceLastPromotion %in% c(1,5,6,7), 1, 0)
data$TopPerformer <- ifelse(data$PerformanceRating == 4, 1, 0)
data$NoStock <- ifelse(data$StockOptionLevel < 1, 1 , 0)
data$NoTraining <- ifelse(data$TrainingTimesLastYear < 1, 1, 0)
data$HourlyOver40 <- ifelse(data$HourlyRate > 40, 1, 0)
data$MonthlyOver15k <- ifelse(data$MonthlyRate > 15000, 1, 0)
data$LogIncome <- log(data$MonthlyIncome)
data$SqIncome <- data$MonthlyIncome^2
data$SqRtIncome <- sqrt(data$MonthlyIncome)


# drop factors for regression analysis
rdata <- subset(data, select = -c(Over18, Department, JobRole, MaritalStatus, EducationField, EmployeeCount, StandardHours))

# scale numerics 0-1 to improve KNN performance
kdata <- data.frame(apply(rdata, MARGIN = 2, FUN = function(X) (X - min(X))/diff(range(X))))

# set the test/train split
splitPerc <- .7

Correlation Analysis

Here we are looking to see improvement gained from feature engineering and to ensure we select features which have high correlation with our response variables (i.e. Income/Attrition) for use in our machine learning algorthims.

Correlation Plot of all Rdata features

data.cor <- cor(rdata)
cdata <- data.cor[,c('Attrition','MonthlyIncome')]
cdata <- data.frame(rbind(names(cdata),cdata))
cdata <- tibble::rownames_to_column(cdata, "Feature")
IncomeCorrelation <- cdata %>% select(Feature, MonthlyIncome) %>% filter(!Feature %in% c('MonthlyIncome',"LogIncome","SqIncome","SqRtIncome")) %>% arrange(abs(MonthlyIncome))

AttritionCorrelation <- cdata %>% select(Feature, Attrition) %>% arrange(abs(Attrition)) %>% filter(Feature != 'Attrition' )
AttritionCorrelation$Feature <- as.factor(AttritionCorrelation$Feature)
IncomeCorrelation %>% top_n(10) %>% mutate(Feature = factor(Feature, Feature)) %>%
  ggplot(aes(Feature,MonthlyIncome, fill=Feature)) + 
  geom_col() + labs(title="Top 10 Monthly Income Drivers") + coord_flip() + 
  scale_fill_discrete(guide = guide_legend(reverse=TRUE))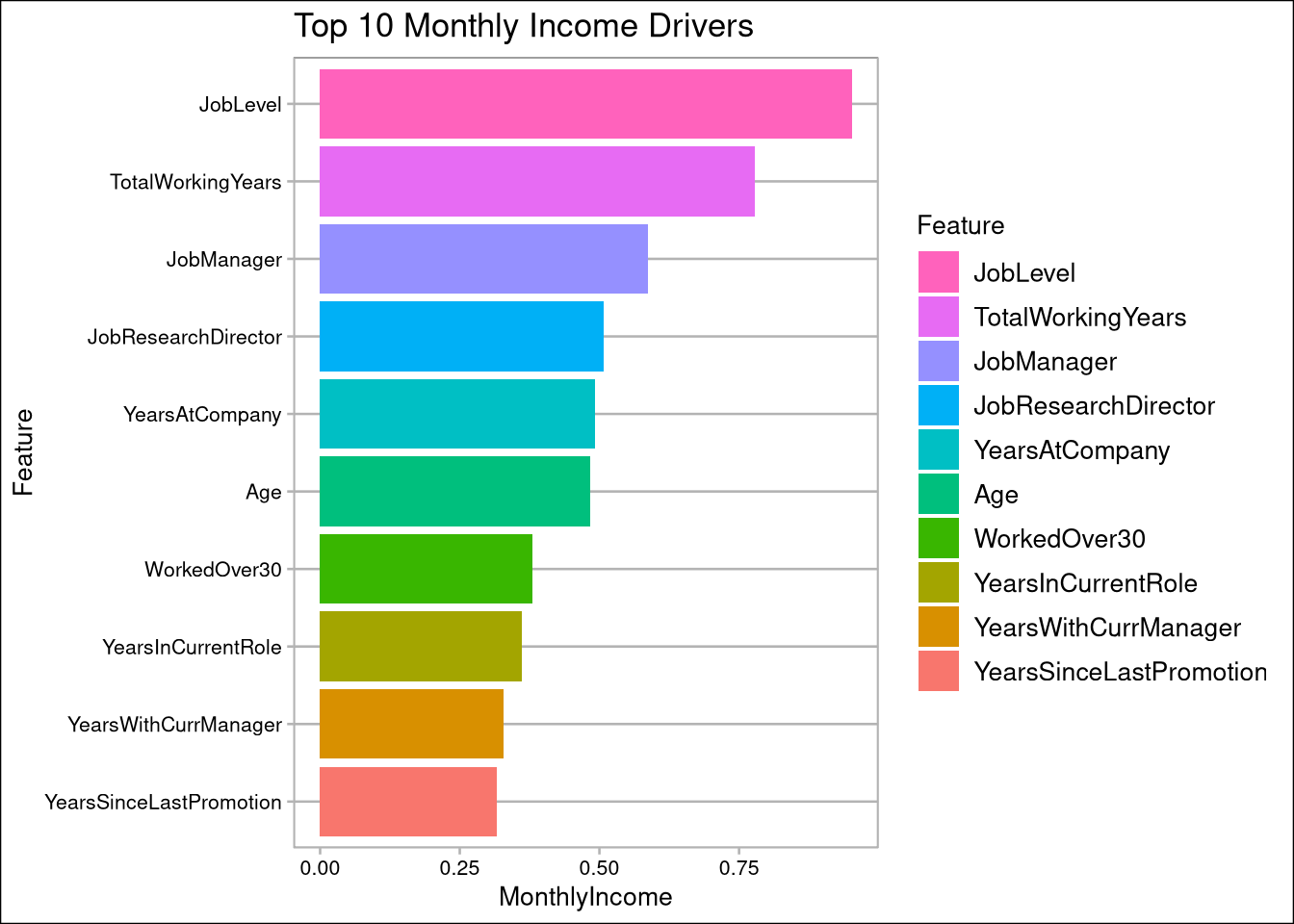

AttritionCorrelation  %>% top_n(10) %>% mutate(Feature = factor(Feature, Feature)) %>%
  ggplot(aes(Feature,Attrition, fill=Feature)) + geom_col() + 
  labs(title="Top 10 Attrition Drivers") + coord_flip() + 
  scale_fill_discrete(guide = guide_legend(reverse=TRUE))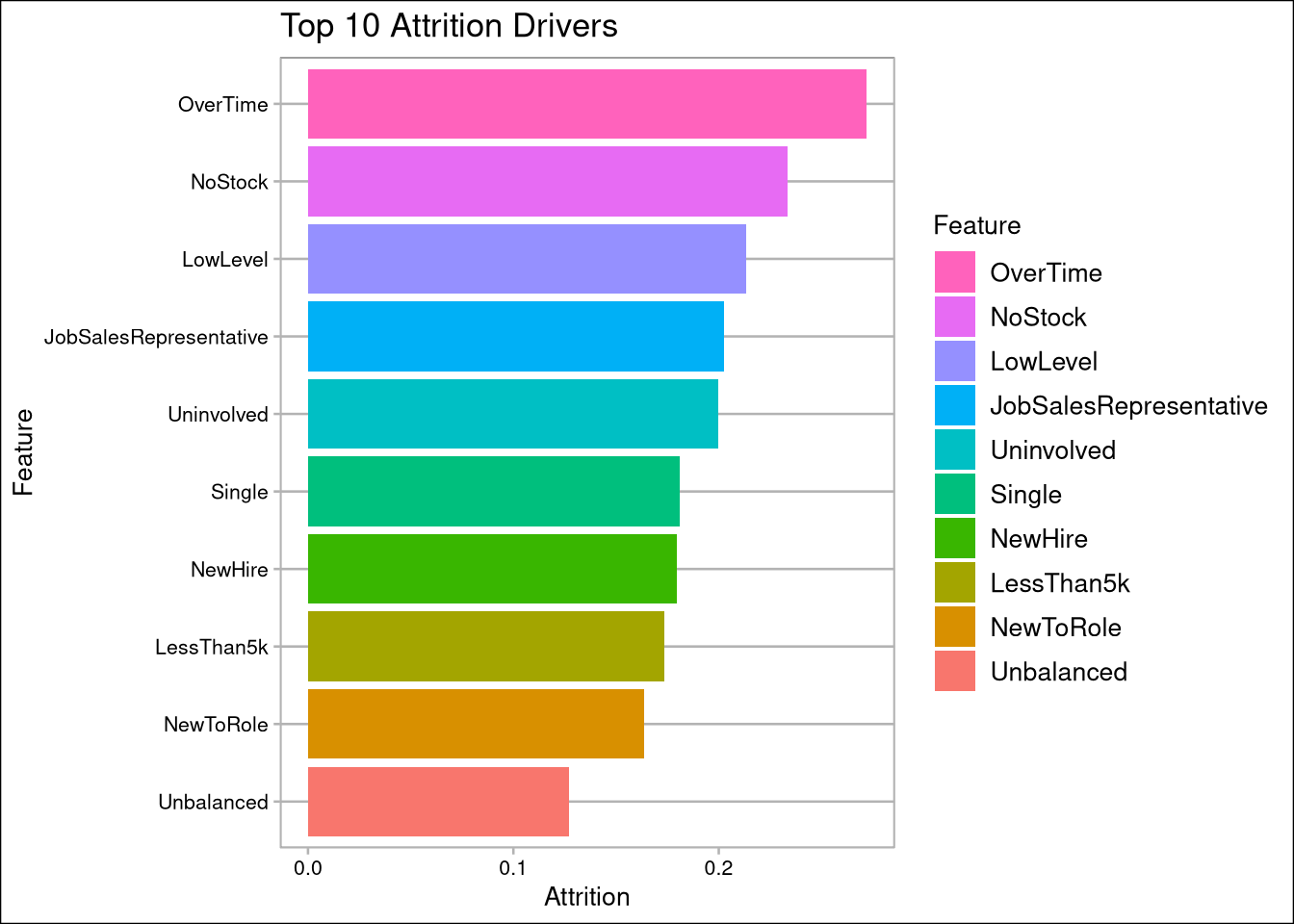

# View correlation for KNN prediction:
data %>% select(
  'Attrition',
  "JobSatisfaction",
  "OverTime",
  "WorkLifeBalance",
  "JobInvolvement",
  "NewHire",
  "DueForPromotion",
  "NoStock",
  "DistanceFromHome",
  "MonthlyIncome"
  ) %>% ggpairs(title = "Correlation for Attrition using KNN Features")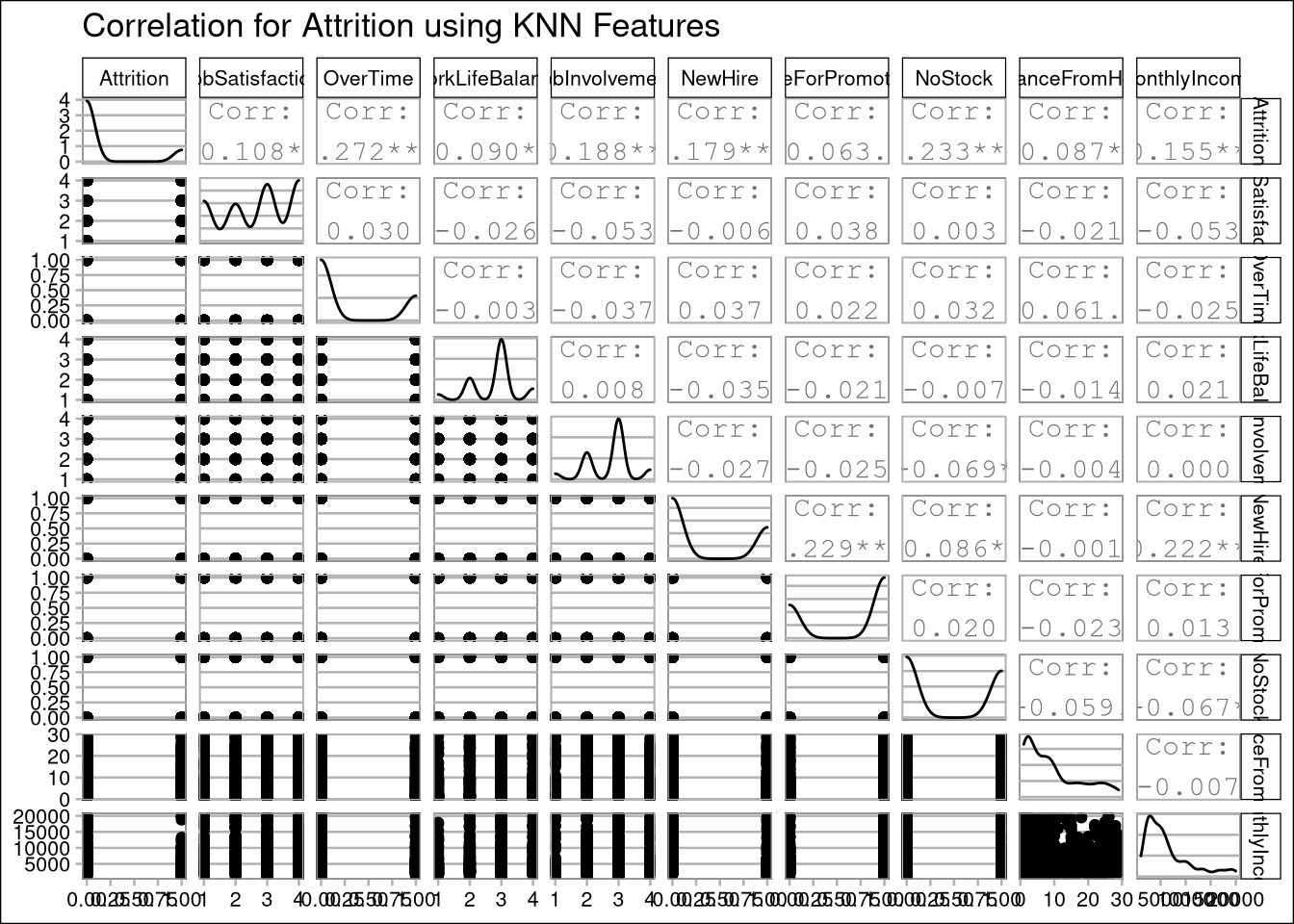

# View correlation plots for salary regression:
data %>% select(
   'MonthlyIncome',
   'JobLevel',
   'TotalWorkingYears',
   'JobRole'
   ) %>% ggpairs(title = "Correlation for Monthly Income using Linear Regression Features")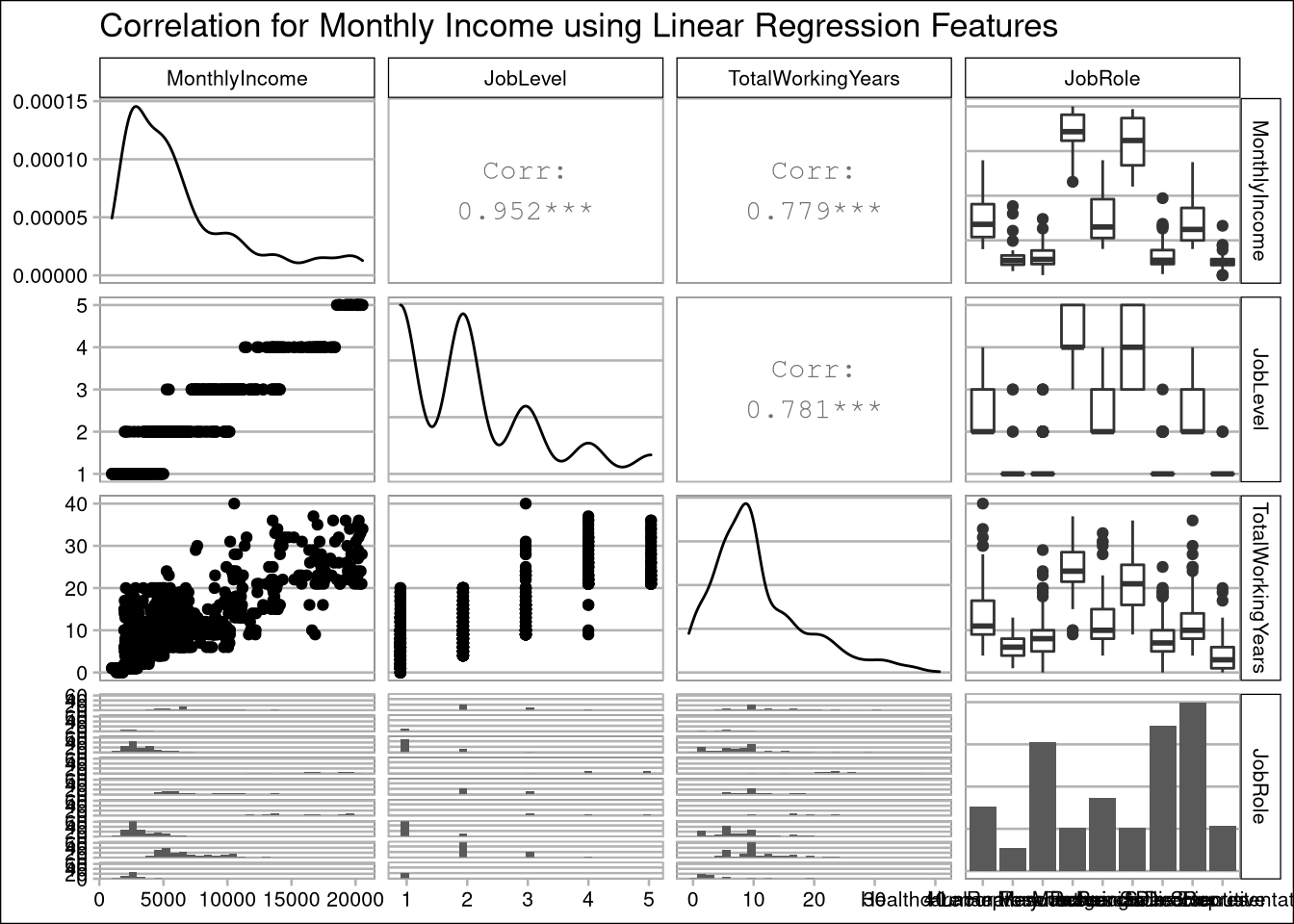

Using K Nearest Neighbors (KNN) to predict employee attrition

First we need to determine the best value of K to use for KNN. We use 50 iterations of tests across all 35 values of K (120% of the square root of the size of the dataset) to find the max useful value of K and the average of its performance statistics.

iterations = 50
set.seed(7)
numks = round(sqrt(dim(kdata)[1])*1.2)
masterAcc = matrix(nrow = iterations, ncol = numks)
masterSpec = matrix(nrow = iterations, ncol = numks)
masterSen = matrix(nrow = iterations, ncol = numks)
knnArray <- c("JobSatisfaction",
              "OverTime",
              "WorkLifeBalance",
              "JobInvolvement",
              "NewHire",
              "DueForPromotion",
              "NoStock",
              "DistanceFromHome",
              "MonthlyIncome"
              )

for(j in 1:iterations) {
  # resample data
  trainIndices = sample(1:dim(kdata)[1],round(splitPerc * dim(kdata)[1]))
  train = kdata[trainIndices,]
  test = kdata[-trainIndices,]
  for(i in 1:numks) {
    # predict using i-th value of k
    classifications = knn(train[,knnArray],test[,knnArray],as.factor(train$Attrition), prob = TRUE, k = i)
    CM = confusionMatrix(table(as.factor(test$Attrition),classifications, dnn = c("Prediction", "Reference")), positive = '1')
    masterAcc[j,i] = CM$overall[1]
    masterSen[j,i] = CM$byClass[1]
    masterSpec[j,i] = ifelse(is.na(CM$byClass[2]),0,CM$byClass[2])

  }
}

MeanAcc <- colMeans(masterAcc)
MeanSen <- colMeans(masterSen)
MeanSpec <- colMeans(masterSpec)
plot(seq(1,numks), MeanAcc, main="K value determination", xlab="Value of K")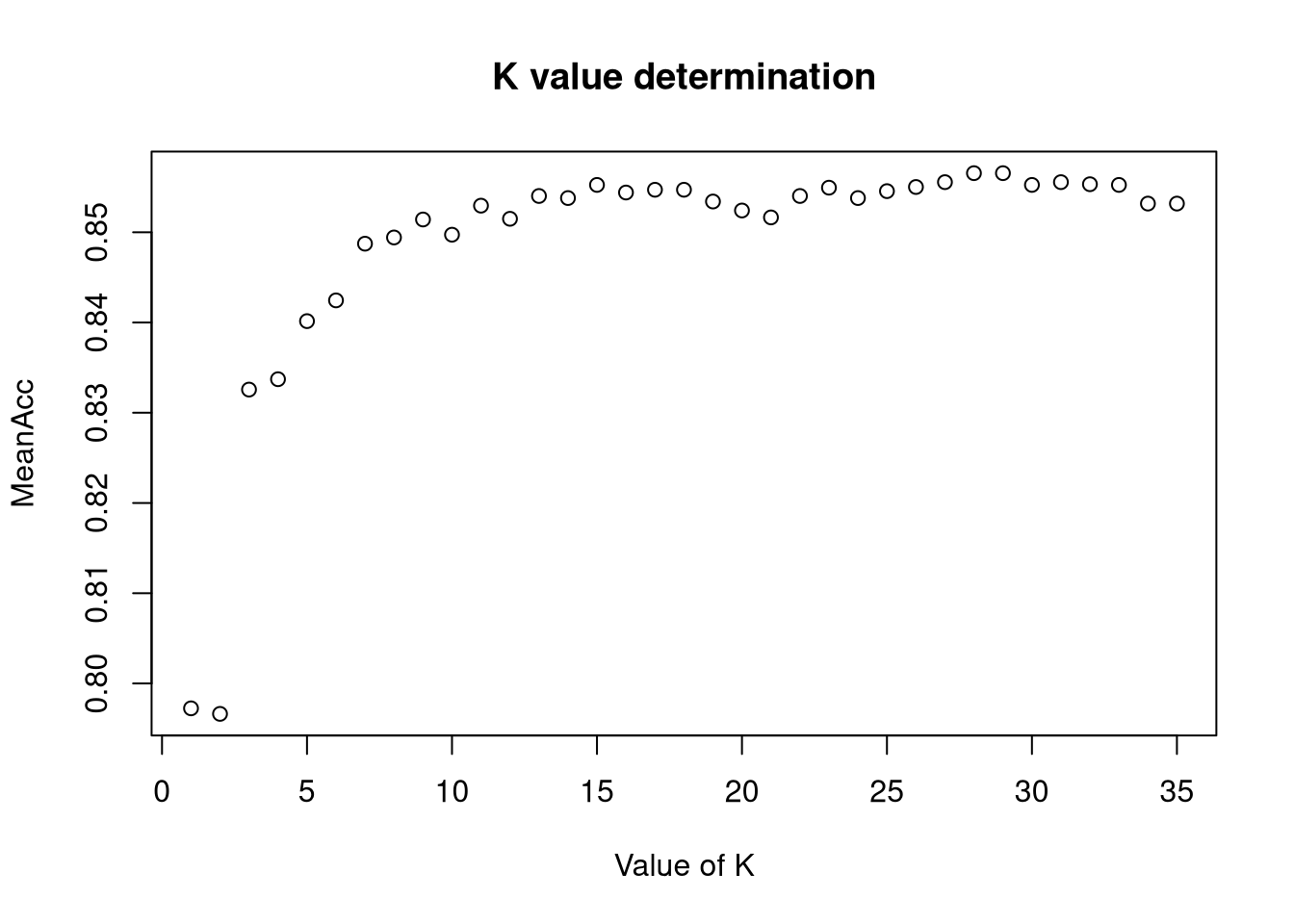

k <- which.max(MeanAcc)
specs <- c(MeanAcc[k],MeanSen[k],MeanSpec[k])
names(specs) <- c("Avg Accuracy", "Avg Sensitivity", "Avg Specificity")
specs %>% kable("html") %>% kable_styling
x
Avg Accuracy 0.8565517
Avg Sensitivity 0.6782740
Avg Specificity 0.8661193 
classifications = knn(train[,knnArray],test[,knnArray],as.factor(train$Attrition), prob = TRUE, k = k)
confusionMatrix(table(test$Attrition,classifications, dnn = c("Prediction", "Reference")), positive = '1')
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   0   1
##          0 215   6
##          1  28  12
##                                           
##                Accuracy : 0.8697          
##                  95% CI : (0.8227, 0.9081)
##     No Information Rate : 0.931           
##     P-Value [Acc > NIR] : 0.9998644       
##                                           
##                   Kappa : 0.3522          
##                                           
##  Mcnemar's Test P-Value : 0.0003164       
##                                           
##             Sensitivity : 0.66667         
##             Specificity : 0.88477         
##          Pos Pred Value : 0.30000         
##          Neg Pred Value : 0.97285         
##              Prevalence : 0.06897         
##          Detection Rate : 0.04598         
##    Detection Prevalence : 0.15326         
##       Balanced Accuracy : 0.77572         
##                                           
##        'Positive' Class : 1               
##

Using Naive Bayes to predict employee attrition

Naive Bayes uses 100 iterations to find an average performance statistics.

iterations = 100
set.seed(7)
masterAcc = matrix(nrow = iterations)
masterSpec = matrix(nrow = iterations)
masterSen = matrix(nrow = iterations)

nbArray <- c("HighlySatisfied", 
             "OverTime", 
             "LowLevel", 
             "Unbalanced",
             "WorkedOver30",
             "JobInvolvement",
             "SalaryHike", 
             "NewHire", 
             "NewToRole",
             "AgeUnder40",
             "DueForPromotion",
             "TopPerformer", 
             "NoStock",
             "MaritalStatus", 
             "LogIncome",
             "MonthlyOver15k", 
             "HourlyOver40")

nbArray <- knnArray

for(j in 1:iterations)
{
  
  trainIndices = sample(1:dim(data)[1],round(splitPerc * dim(data)[1]))
  train = data[trainIndices,]
  test = data[-trainIndices,]
  model = naiveBayes(train[,nbArray],as.factor(train$Attrition),laplace = .0001)
  CM = confusionMatrix(table(predict(model,test[,nbArray]),as.factor(test$Attrition), dnn = c("Prediction", "Reference")), positive = '1')
  masterAcc[j] = CM$overall[1]
  masterSen[j] = CM$byClass[1]
  masterSpec[j] = CM$byClass[2]

}
specs <- c(colMeans(masterAcc),colMeans(masterSen),colMeans(masterSpec))
names(specs) <- c("Avg Accuracy", "Avg Sensitivity", "Avg Specificity")
specs %>% kable("html") %>% kable_styling
x
Avg Accuracy 0.8617241
Avg Sensitivity 0.4044971
Avg Specificity 0.9505032 
confusionMatrix(table(predict(model,test[,nbArray]),as.factor(test$Attrition), dnn = c("Prediction", "Reference")), positive = '1')
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   0   1
##          0 195  28
##          1  18  20
##                                         
##                Accuracy : 0.8238        
##                  95% CI : (0.772, 0.868)
##     No Information Rate : 0.8161        
##     P-Value [Acc > NIR] : 0.4115        
##                                         
##                   Kappa : 0.3613        
##                                         
##  Mcnemar's Test P-Value : 0.1845        
##                                         
##             Sensitivity : 0.41667       
##             Specificity : 0.91549       
##          Pos Pred Value : 0.52632       
##          Neg Pred Value : 0.87444       
##              Prevalence : 0.18391       
##          Detection Rate : 0.07663       
##    Detection Prevalence : 0.14559       
##       Balanced Accuracy : 0.66608       
##                                         
##        'Positive' Class : 1             
##

Using Fast Naive Bayes to predict employee attrition

The Fast Naive Bayes method below uses 100 iterations to find average performance statistics using only binary features.

iterations = 100
set.seed(7)
masterAcc2 = matrix(nrow = iterations)
masterSpec2 = matrix(nrow = iterations)
masterSen2 = matrix(nrow = iterations)

nbArray2 <- c("OverTime", 
              "LowLevel",
              "HighlySatisfied",
              "Unbalanced",
              "WorkedOver30",
              "SalaryHike", 
              "NewHire",
              "NewToRole", 
              "AgeUnder40",
              "DueForPromotion",
              "TopPerformer",
              "NoStock",
              "Gender",
              "Uninvolved", 
              "Single",
              "Divorced",
              "Married",
              "LongCommute",
              "NoTraining",
              "HourlyOver40",
              "MonthlyOver15k",
              "JobManager",
              "JobSalesExecutive", 
              "JobSalesRepresentative")

for(j in 1:iterations)
{
  
  trainIndices = sample(1:dim(rdata)[1],round(splitPerc * dim(rdata)[1]))
  train2 = rdata[trainIndices,]
  test2 = rdata[-trainIndices,]
  model2 = fnb.bernoulli(train2[,nbArray2], train2$Attrition, laplace = .0001)
  CM2 = confusionMatrix(table(predict(model2,test2[,nbArray2]),as.factor(test2$Attrition), dnn = c("Prediction", "Reference")), positive = '1')
  masterAcc2[j] = CM2$overall[1]
  masterSen2[j] = CM2$byClass[1]
  masterSpec2[j] = CM2$byClass[2]
}
specs <- c(colMeans(masterAcc2),colMeans(masterSen2),colMeans(masterSpec2))
names(specs) <- c("Avg Accuracy", "Avg Sensitivity", "Avg Specificity")
specs %>% kable("html") %>% kable_styling
x
Avg Accuracy 0.8558238
Avg Sensitivity 0.4981112
Avg Specificity 0.9254531 
confusionMatrix(table(predict(model2,test2[,nbArray2]),as.factor(test2$Attrition), dnn = c("Prediction", "Reference")), positive = '1')
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   0   1
##          0 190  24
##          1  23  24
##                                           
##                Accuracy : 0.8199          
##                  95% CI : (0.7678, 0.8646)
##     No Information Rate : 0.8161          
##     P-Value [Acc > NIR] : 0.4749          
##                                           
##                   Kappa : 0.3952          
##                                           
##  Mcnemar's Test P-Value : 1.0000          
##                                           
##             Sensitivity : 0.50000         
##             Specificity : 0.89202         
##          Pos Pred Value : 0.51064         
##          Neg Pred Value : 0.88785         
##              Prevalence : 0.18391         
##          Detection Rate : 0.09195         
##    Detection Prevalence : 0.18008         
##       Balanced Accuracy : 0.69601         
##                                           
##        'Positive' Class : 1               
##

Using Logistic Regression to predict employee attrition

set.seed(7)
trainIndices = sample(1:dim(data)[1],round(splitPerc * dim(data)[1]))
train = data[trainIndices,]
test = data[-trainIndices,]
model3 <- glm(Attrition ~ JobSatisfaction + 
                OverTime + 
                WorkLifeBalance + 
                JobInvolvement + 
                NewHire + 
                NoStock + 
                BusinessTravel +
                DistanceFromHome +
                YearsSinceLastPromotion +
                EnvironmentSatisfaction
              , data=train, family="binomial")

#HourlyRate+NewToRole +NumCompaniesWorked+LogIncome+JobRole
summary(model3)
## 
## Call:
## glm(formula = Attrition ~ JobSatisfaction + OverTime + WorkLifeBalance + 
##     JobInvolvement + NewHire + NoStock + BusinessTravel + DistanceFromHome + 
##     YearsSinceLastPromotion + EnvironmentSatisfaction, family = "binomial", 
##     data = train)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.9646  -0.5692  -0.3528  -0.2028   2.9072  
## 
## Coefficients:
##                         Estimate Std. Error z value Pr(>|z|)    
## (Intercept)             -0.22404    0.81878  -0.274  0.78437    
## JobSatisfaction         -0.36064    0.11198  -3.220  0.00128 ** 
## OverTime                 1.45197    0.25085   5.788 7.12e-09 ***
## WorkLifeBalance         -0.30413    0.17454  -1.742  0.08143 .  
## JobInvolvement          -0.70384    0.17417  -4.041 5.32e-05 ***
## NewHire                  1.09192    0.27736   3.937 8.26e-05 ***
## NoStock                  1.21630    0.25697   4.733 2.21e-06 ***
## BusinessTravel           0.54487    0.23629   2.306  0.02112 *  
## DistanceFromHome         0.02715    0.01469   1.848  0.06457 .  
## YearsSinceLastPromotion  0.08097    0.03952   2.049  0.04050 *  
## EnvironmentSatisfaction -0.17431    0.11485  -1.518  0.12910    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 553.59  on 608  degrees of freedom
## Residual deviance: 429.64  on 598  degrees of freedom
## AIC: 451.64
## 
## Number of Fisher Scoring iterations: 5
atPrd <- predict(model3, type="response", newdata = test)
actualPred <- ifelse(atPrd > 0.5, 1, 0)
confusionMatrix(table(as.factor(actualPred), as.factor(test$Attrition), dnn = c("Prediction", "Reference")), positive = '1')
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   0   1
##          0 218  21
##          1   6  16
##                                           
##                Accuracy : 0.8966          
##                  95% CI : (0.8531, 0.9307)
##     No Information Rate : 0.8582          
##     P-Value [Acc > NIR] : 0.041690        
##                                           
##                   Kappa : 0.4883          
##                                           
##  Mcnemar's Test P-Value : 0.007054        
##                                           
##             Sensitivity : 0.43243         
##             Specificity : 0.97321         
##          Pos Pred Value : 0.72727         
##          Neg Pred Value : 0.91213         
##              Prevalence : 0.14176         
##          Detection Rate : 0.06130         
##    Detection Prevalence : 0.08429         
##       Balanced Accuracy : 0.70282         
##                                           
##        'Positive' Class : 1               
##

Using Multiple Linear Regression to predict monthly income

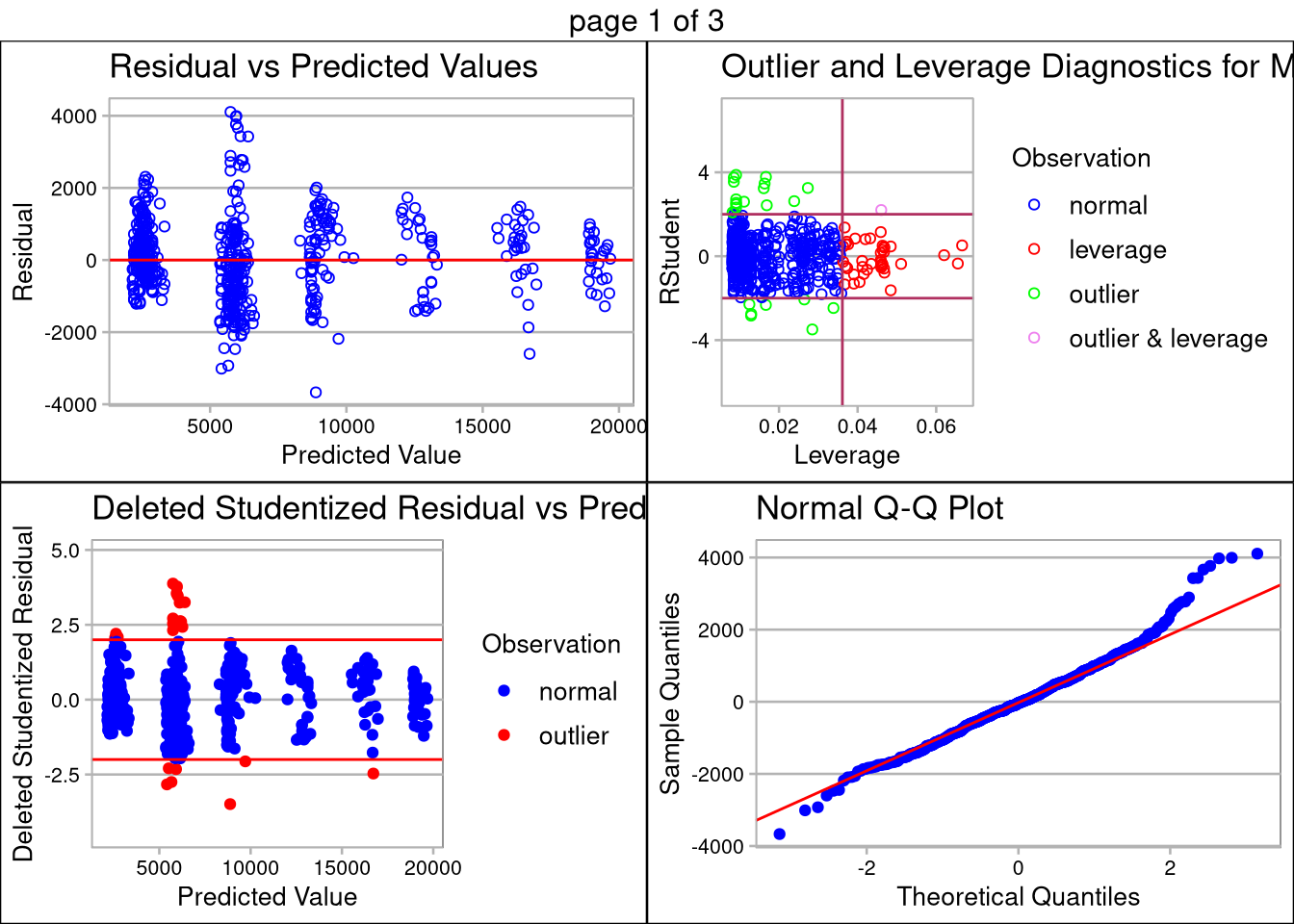
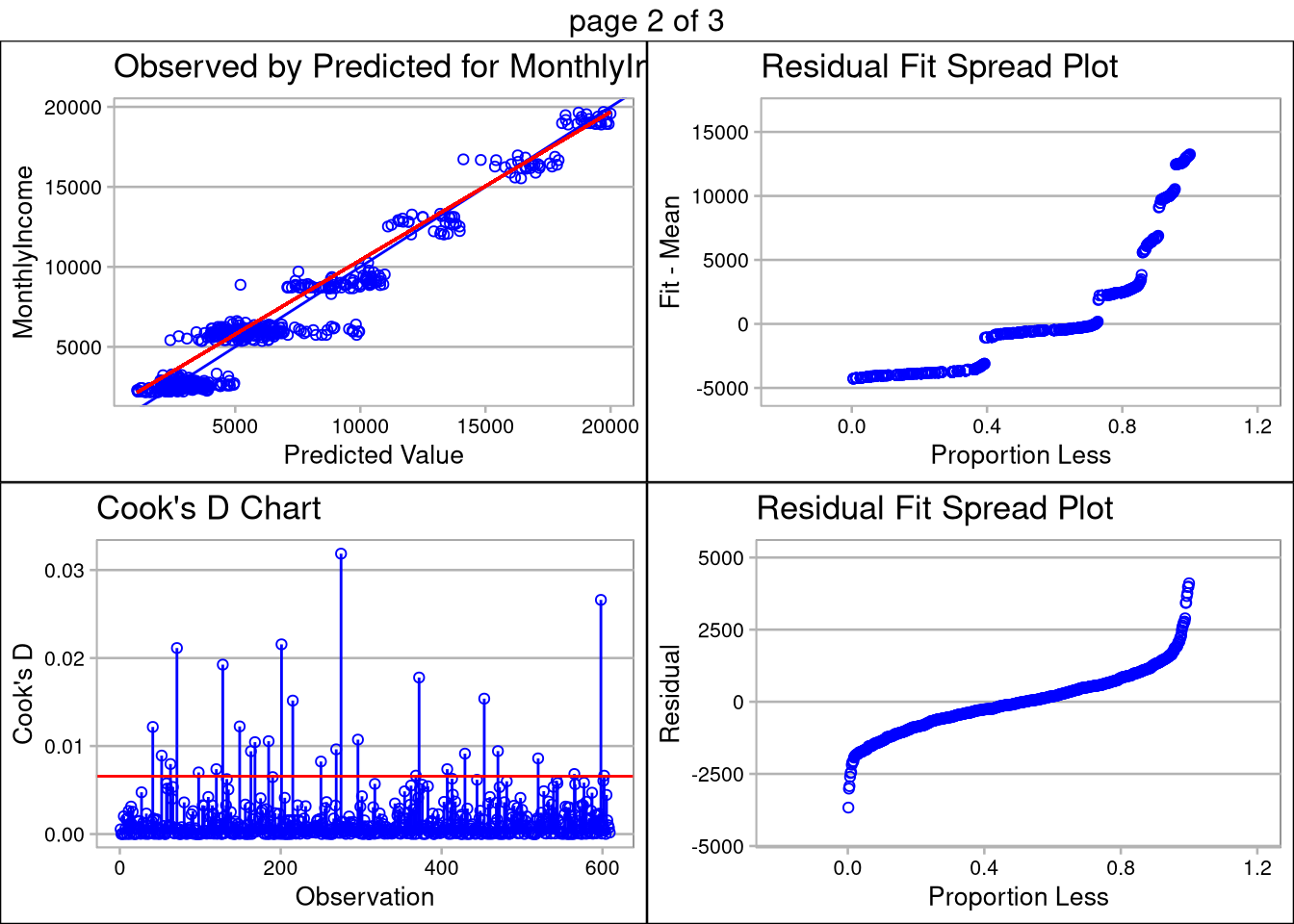
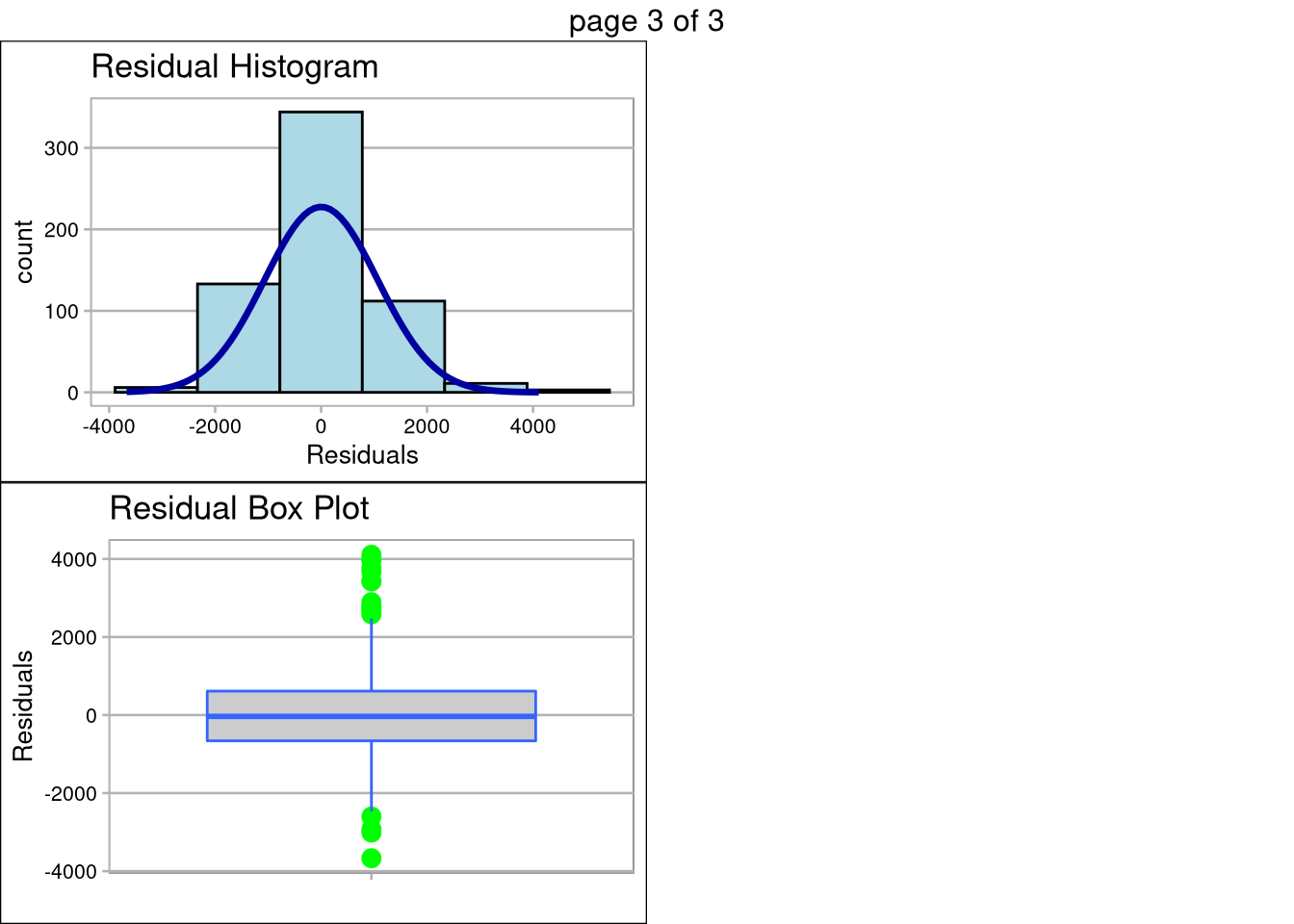
Multiple linear regression is sensitive to co-linearity of features. Using the correlation matrix above, we determined the simplest model uses only JobLevel, TotalWorkingYears, and JobRole for prediction. The TotalWorkingYears and JobLevel features are both highly significant (p-values <.0001) and have a large impact on the estimated salary regression line.

The plot below the prediction summary validates the assumptions of linear regression are met. The data appears normally distributed (as seen in the QQ Plot), the features are linearly correlated, there are no extreme outliers with high influence, and standard deviation among the plots is equal less a few outliers. Transformation of the data did not help with the inequality of variance, so caution should be used when making inference on monthly salary, especially n the ~$5,000/month range.

set.seed(7)
  trainIndices = sample(1:dim(rdata)[1],round(splitPerc * dim(rdata)[1]))
  train = data[trainIndices,]
  test = data[-trainIndices,]
salFit <- lm(MonthlyIncome ~ 
               JobLevel + 
               TotalWorkingYears +
               JobRole 
             ,data=train)
summary(salFit)
## 
## Call:
## lm(formula = MonthlyIncome ~ JobLevel + TotalWorkingYears + JobRole, 
##     data = train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3669.2  -661.0   -34.7   613.6  4106.0 
## 
## Coefficients:
##                               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                    -25.671    260.270  -0.099  0.92146    
## JobLevel                      2762.115     98.253  28.112  < 2e-16 ***
## TotalWorkingYears               49.968      9.242   5.407 9.29e-08 ***
## JobRoleHuman Resources        -409.005    297.717  -1.374  0.17002    
## JobRoleLaboratory Technician  -580.693    217.614  -2.668  0.00783 ** 
## JobRoleManager                4097.501    277.600  14.760  < 2e-16 ***
## JobRoleManufacturing Director  116.621    206.533   0.565  0.57252    
## JobRoleResearch Director      4059.775    264.269  15.362  < 2e-16 ***
## JobRoleResearch Scientist     -357.981    216.054  -1.657  0.09806 .  
## JobRoleSales Executive         -50.411    186.455  -0.270  0.78697    
## JobRoleSales Representative   -494.479    263.957  -1.873  0.06151 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1077 on 598 degrees of freedom
## Multiple R-squared:  0.9483, Adjusted R-squared:  0.9474 
## F-statistic:  1096 on 10 and 598 DF,  p-value: < 2.2e-16
salPrd <- predict(salFit, interval="predict",newdata = test)
RMSE <- sqrt(mean((salPrd[,1] - test$MonthlyIncome)^2))
RMSE
## [1] 1033.745
olsrr::ols_plot_diagnostics(salFit)